프랙탈(Fractal)은 카오스에 내재한 질서 구조이자 그것을 묘사할 수 있는 언어라고 할 수 있으며, 카오스가 복잡하면서도 그 속에 하나의 질서를 지니는 것은 프랙탈이 있기 때문이다. 프랙탈은 고사리처럼 부분이 전체를 닮은 모양을 하고 있으면서(자기 유사성), 이런 닮는 과정을 끊임없이 반복하는(순환성) 특징을 지니고 있다.

주변의 나무 모습을 살펴보면 나무 위로 떨어지는 햇빛을 조금이라도 낭비하지 않고 광합성에 이용wjsjf할 수 있도록 나뭇잎이 조금도 빈틈없이 나무 전체를 뒤덮고 있음을 알 수 있다.

나뭇잎이 이렇게 나무 전체를 뒤덮기 위해서는 나무의 잔가지들이 모든 방향으로 골고루 나 있어야 한다. 그렇다면 과연 나무의 무엇이 잔가지들의 방향을 통제하여 모든 방향으로 골고루 향하도록 해줄까? 복잡하게 얽힌 나뭇가지를 보면서 나뭇가지의 기하학적 구조가 매우 복잡할 것이라고 생각할 수가 있다.

그러나 사실 이런 나뭇가지의 형태는 매우 간단한 규칙으로부터 만들어진다. 나뭇가지가 일정한 길이의 비(比)가 될 때마다 두 개의 가지로 갈라진다고 하는 간단한 규칙만으로도 모든 방향으로 뻗은 나뭇가지의 구조를 만들어 낼 수가 있다.

이 경우에 가지의 어느 부분을 선택하여 확대를 해도 전체 나무 모양과 같은 모양을 얻을 수 있다. 이러한 성질을 '자기 유사성(Self-Similarity)'이라고 하며, 자기 유사성을 갖는 기하학적 구조를 프랙탈 구조라고 한다.

허파에서 동맥이 갈라져서 실핏줄을 이루는 구조 역시 프랙탈 구조의 예이다. 허파로 들어오는 하나의 동맥은 계속 갈라져서 공기와 실핏줄의 접촉면을 최대로 하여 가장 효율적으로 산소 교환이 일어날 수 있도록 하는 허파꽈리를 형성하게 되는 것이다.

고사리와 같은 양치류 식물, 아름다운 눈송이의 구조, 우주의 신비스런 모습, 하천의 흐름, 산맥의 지형, 너울이 밀려오는 해안선의 모습, 새하얀 뭉게구름의 형상 등 주변의 많은 것들에서 우리는 프랙탈 구조를 쉽게 발견할 수가 있다. 그러나 이 세상에서 완전히 똑같은 것은 없다. 다만 우리가 같은 류(類)에 관한 자기닮음을 직관적으로 인식하기에 같은 것으로 보이는 것이다.

프랙탈(fractal) 용어는 1975년 IBM 연구원으로 있던 만델브로트(Benoit B. Mandelbrot)에 의해 처음으로 고안되었지만, 이와 유사한 개념은 그전부터 이미 있어왔다. 만델브로트는 1967년 미국의 저명한 과학저널 『사이언스(Science)』에 「영국을 둘러싸고 있는 해안선의 총 길이는 얼마인가」라는 논문을 통해 프랙탈 이론을 설명한 바가 있다. 이 논문에서 그는 영국의 프랙탈적인 해안선(리아스식 해안선)의 길이는 어떤 단위의 자(尺)로 재느냐에 따라 얼마든지 달라질 수 있다고 주장했으며 실제로 이를 증명도 하였다.

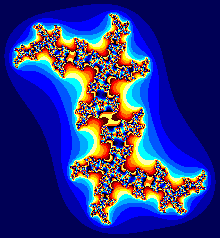
프랙탈은 자기 유사성(Self-Similarity)을 전제로 끊임없이 자기 복제를 반복하는 순환성(Recursiveness)의 특성을 가지는데, 이는 아주 간단한 수학식인 z=z²+c에서 출발한다. Z와 C는 복소수(complex number, 실수와 허수의 합으로 이루어지는 수)라는 점을 제외하면 아주 간단한 수학식이다. 이 간단한 수학식에서 만델브로트 집합, 줄리아 집합이라고 하는 광활한 우주가 만들어졌으며, 그 속에는 아무도 상상할 수 없었던 기상천외한 많은 것들이 수없이 많이 감추어져 있다.

그리고 프랙탈은 자기 유사성, 순환성 외에 알고리즘의 단순성이라는 특징도 가지고 있다. 즉 '수학식 z=z²+c의 반복 계산 결과 Z가 발산하느냐 수렴하느냐'와 '허수 i²=-1'이라는 것이 논리의 전부이다.

만델브로트의 구체적인 관심사는 그의 단순한 방정식에서 나오는 값의 증가였다. 그는 어떤 C값에서는 방정식에서 나오는 허수(i)의 값이 계속 증가할 것임을 알았다. 그러나 다른 C값에서 그 허수의 값은 아주 작은 두 허수 사이를 왕복한다. 그래서 그는 컴퓨터를 이용, 허수 값이 무한히 발산하지 않는 각각의 C값을 화면 위에 점으로 표현했다.

그 결과 만델브로트 집합이라는 그림이 나왔다. 납작하게 눌린 벌레의 가장자리에 수많은 촉수가 달린 모습이었고, 어떻게 보면 잉크 얼룩과도 같았다. 그것은 정사각형이나 정삼각형, 원 같은 순수한 기하학적 형태와는 거리가 먼, 뚜렷한 유기적 형태였다.

만델브로트는 그림이 너무 이상한 나머지 그것을 계속 확대해보았으나 단지 더 세부적인 형태만 나왔다. 계속 확대해 들어가도 보이는 것은 더 복잡한 구조뿐이었다. 만델브로트 집합의 세부적 형태는 끝없이 계속된다는 사실이 곧 분명해졌다. 그것을 영원히 확대해도 같은 모양의 구조가 계속 나올 것이다. 프랙탈 기하학은 고전적 기하학에서와 달리 특정된 크기나 축척이 큰 영향을 미치지 않는다는 사실을 알게 된 것이다.

만델브로트 집합과 함께 프랙탈의 양대 산맥을 형성하는 줄리아 집합은 만델브로트 집합이 나타나기 훨씬 전인 1918년 프랑스의 수학자인 줄리아(Gaston Julia)에 의해 발표되었다. 만델브로트가 프랙탈의 아버지라면 줄리아는 프랙탈의 할아버지에 해당한다. 만일 줄리아 집합이 발표될 당시 그래픽 기능이 있는 컴퓨터가 있었다면 줄리아 집합이 화려한 명성을 먼저 누렸을 것이다. 수학식 z=z²+c에서 Z를 발산시키지 않는 C값들의 모임이 만델브로트 집합이라면, C값을 고정시킨 상태에서 Z를 발산시키지 않는 Z값들의 모임이 줄리아 집합이다.

프랙탈 구조는 자연물에서 뿐만 아니라 수학적 분석, 생태학적 계산, 위상공간에 나타나는 운동모형 등 곳곳에서도 발견되어 자연이 가지는 기본적인 구조라는 사실도 깨닫게 되었다. 따라서 우리는 프랙탈 구조에 대한 이해를 통하여 불규칙하며 혼란스러워 보이는 현상을 배후에서 지배하는 규칙도 찾아낼 수 있게 되었다. 이제 프랙탈 구조는 혼란스러워 보이는 현상을 설명하는 새로운 언어로 등장하게 되었다.

   프랙탈의 형상

   보다 자세한 사항은 참고 자료에서 찾아주세요!!

up↑

Copyrightⓒ2004~ @FRACTAL. All rights reserved.